Peak-to-peak and RMS jitter

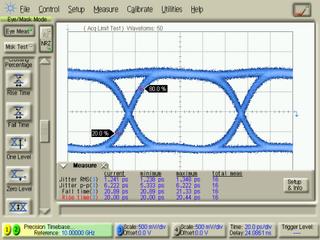What does jitter mean? Jitter is very common word in oscillatory systems vocabulary. In an ideal oscillator, time difference between transitions (for example two rising or falling edges) is constant. In practice, due to existence of noise these spacings are varying. Assume Vout is referred as output voltage of an oscillator and t(n) as the time point of the nth zero crossing of rising edge of Vout. The nth period of Vout can be defined as T(n)=t(n+1)-t(n). As we mentioned earlier, this difference is constant for an ideal oscillator but not in a practical one. This variation in T(n) can be called as jitter. If T(n) is deviated from mean period (Tm), then we can define: d(T)=T(n)-Tm.

The RMS value of d(T) for infinite number of cycles is called as "RMS jitter" while the difference between maximum and minimum value of d(T) is called as "peak-to-peak jitter". For more detailed definitions and calculations refer Yamaguchi et al.

On the other hand random jitter can be specified by Gaussian distribution. Standard deviation of this distribution gives RMS jitter. If Bit Error Rate (BER) of a jittery system is specified, the relationship between RMS and peak-to-peak (pp) value of jitter can be written as:

Jitter(pp)=k* Jitter(RMS)

where k is BER-dependent constant and can be calculated by solving following equation:

0.5*erfc(k/(8^0.5))=BER. (in "x^y" y is power for x)

In this equation erfc(x) is "error function" and it is tabulated in different references. Using such a table gives the values for k. For example:

BER=10^-3.......k=6.18

BER=10^-6.......k=9.5

BER=10^-12.....k=14

In measurements BER=10^-12 will cover 99.99999% of time interval of Gaussian distribution to calculate pp value of jitter.